14 : What the Algorithm!

Random fact

The Comic Sans font came from an actual comic book.

Most adults nowadays who know anything about graphic design steer away from using the Comic Sans font in formal documents. The font was designed by Vincent Connare, who drew direct inspiration from his favorite comic books, including Alan Moore and Dave Gibbons' celebrated Watchmen series.

Introduction

Algorithms are important as they have enabled technology to progress.

As tech hardware has progressed, we are now producing and consuming more data than ever before. Improvements in the algorithms we use in our systems has been key to allowing us to progress.

There is only so far computer hardware can go - even the worlds super computers will take time to run a poor performing algorithm, where a more efficient version of that algorithm would take a fraction of the time on run-of-the-mill hardware.

Algorithms and data structures really matter in a computer engineering context!

Without efficient Algorithms we wouldn’t be where we are today in terms of our digital capability. So lets talk Algorithms!

• Linus Torvalds quote:
  • Bad programmers worry about the code. Good programmers worry about data structures and their relationships.

Algorithm - what do you mean - like A + B = C ???

An algorithm is a set of well defined instructions for solving a task or a computational problem

Use them all the time in everyday life - making a cup of tea, cooking, sorting, directions.

In computing Algorithms go hand in hand with data structures.

Data structures

Primitive data types:

• Tend to be value types like:
  • bool, byte, int, long, float, decimal
• Reference types:
  • string - immutable (can’t be changed once created)
  • Array - constant time to access by index

Data abstraction:

• we could write all of our programs with just the primitive types, but we don’t, we add higher levels of abstraction, which has given rise to different styles of programming:
  • Object Oriented Programming
  • Functional Programming
  • Structured Programming
• In OOP, classes provide a means of abstraction, which make way for more complex reference data types.
  • In OOP, you don't need to know how the operation works to be able to use it, you just need to call the api - the hard stuff is abstracted away
  • a set of values and a set of operations on those values
  • BUT this could get you into a world of pain unless you know the time complexity related to each

Time complexity - how an algorithms execution time changes relative to the input size, worst case - more stuff going in it’s going to be slower

• General categories are, fastest to slowest. N is the size of the input, aka number of items:
  • O(1) - “constant time” - always the same time to execute no matter how big the input
    • Plucking an item from a list using an index or a key: O(1)
  • Time grows as the size of the input grows

    • Desirable

      • O(logn) - “log n” - takes logarithm base 2 times the number of items input (n)
        • Divide and conquer algorithms
        • logarithms is the inverse of ‘to the power of’ so grows very slowly, whereas ‘to the power of’ grows exponentially
        • Examples - binary search is a good example - requires data to be sorted though
        • Really the Holy Grail of algorithm time complexity
        • Example: Let’s say we have 1000 items. To find a specific item we will need to do 1000 operations (comparing a property in each item). But how many will it do if we use an binary search? I need to find the log base 2 (because of the binary split) of 1000: 9.96 (10) - how many operations will be needed if we have a million records (it’s 20) or a billion (it’s 30). Splitting down the middle and then testing
      • O(n) - “linear” - time increases proportional to the input - iterating over an entire collection
      • O(nlogn) - “nlogn” - logn, but done n times, ie one for each input item

    • Undesirable:

      • O(n^2) - “quadratic” - n times n - nested loop for each item - bubblesort
      • O(2^n) - “exponential” - brute force algorithms, multiple iterations of input items - time double with each new item of input

      

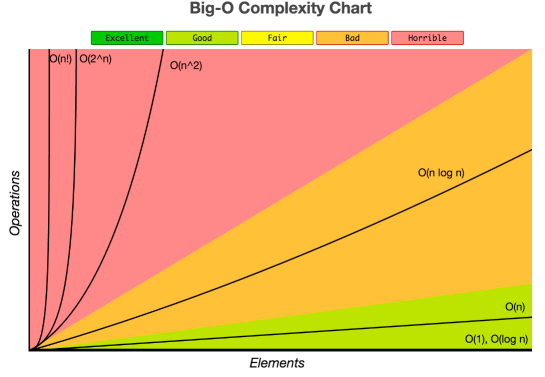
      Originally from https://biercoff.com/big-o-complexity-cool-cheat-sheet/

Good reference for common data structure operation time complexity (search, insertion, deletion times) - https://biercoff.com/big-o-complexity-cool-cheat-sheet/ & https://www.bigocheatsheet.com/

More complex data structures that have operations associated with them:

• Examples data types are: -
  • For algorithms, lets have a closer look at collection types. these have interesting operations where the inner workings of the algorithm really make a difference, mostly implemented with arrays under the hood:
    • Bags
    • Lists
      • array that is resized in blocks as you add stuff
    • Linked Lists
      • array but with pointers to other items
      • or simple class with pointers forward
    • Queues
      • FIFO - First in first out
        • enqueue/dequeue
        • built on array - there is an implementation where dequeue takes item at index[0]
      • Priority queues
        • Data is sorted as it is added
          • read operation is constant
          • insertion operation - logn (using heaps)
    • Stacks
      • LIFO - Last in first out - push/pop
      • built on array - there is an implementation where pop takes the last item in the array
    • Trees
      • Binary tree - efficient at storing and retrieving data
    • Graphs - directed and undirected, weighted
    • HashMaps (Dictionaries)
      • constant time to access by key - how does this work?
        • array is used under the covers
        • key is hashed to an index (using a constant time hashing algo), item at index is retrieved
          • How hashing clashes are handled - Multiple keys can hash to same index, collision handling is implemented where each index is a collection, which is then efficiently searched

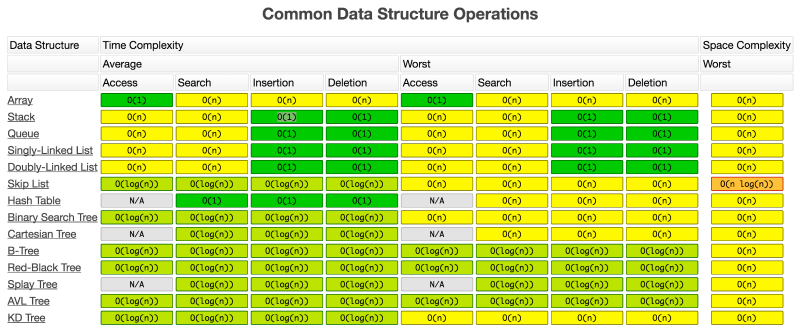
Originally from https://biercoff.com/big-o-complexity-cool-cheat-sheet/

Key algorithms

• useful ones to look at

• Sorting

  • Bubblesort - quadratic, easy to think through, each item is compared with every other item
  • Mergesort - nlogn
    • divide and conquer
    • created by John von Neumann in 1945
    • does not mutate the existing array, uses extra array
  • Quicksort - nlogn, n^2 in worst case, depending on how data is initially partitioned.
    • divide and conquer
    • superior to merge sort - generally accepted to be superior to merge sort
      • better in many scenarios
      • generally fewer swaps necessary in most screnarios
    • in place sorting - mutates the existing array
    • Created by Tony Hoare in 1960
    • This is default sort in .Net
  • Sorting algorithms are used in insert Priority Queue data structures

  

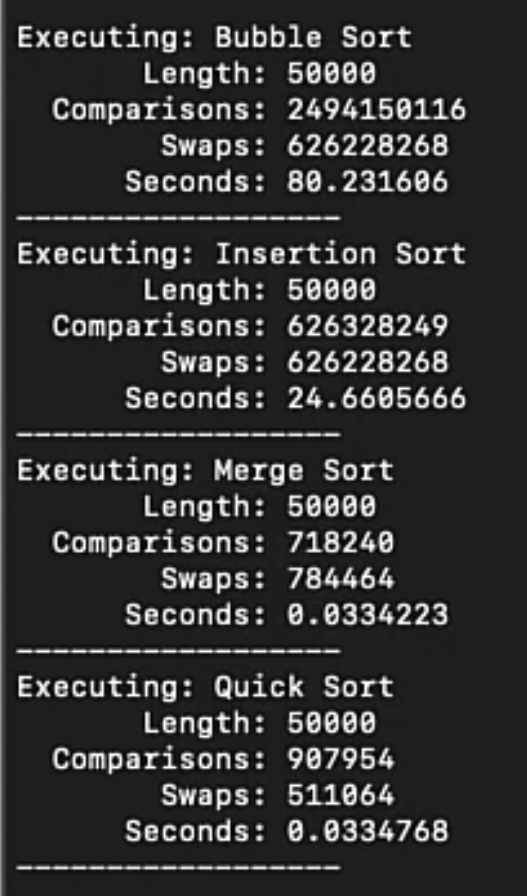
• Searching

  • Binary search - logn
  • Sequential search - linear - n
  • Binary Search Trees / Balanced Search Trees / Red-Black BSTs - logn

• Graphs - used in many areas of life from social networks, to viral spread modelling, computer networking like the internet!, resource allocation in an operating system

  • Undirected
    • Depth first search - finding your way through a maze
      • Uses a stack (or recursive if graph not too big)
    • Breadth first search - simple shortest path algorithms
      • Differs only from DFS - in the data structure that is used!
        • Genius really!
        • uses a queue
    • Connected components - areas in a graph that are connected to determine components
    • Degrees of separation - Kevin Bacon? 🙂
  • Directed
    • Direct cycle detection
    • Topological sorting
    • Strong connectivity
  • Weighted
    • Shortest path - in a weighted context

• Strings

  • string sorts
  • substring search
  • regular expressions
  • data compression

Last time you had to write/implement an algorithm?

Reasons you would have to implement one - breaking new ground, something nobody else is doing

Useful to understand how they are implemented - gives you and insight and understanding and knowledge of the right tool for the job

Interesting to play with and learn from -

Code Kata, Code Wars, LeetCode

Calculate Prime numbers (https://en.wikipedia.org/wiki/Sieve_theory)

The sieve of Eratosthenes hacked up in C#:

   var n = 30;
   Console.WriteLine($"Prime numbers to {n}");
   var marked = Enumerable.Repeat(true, n+1).ToArray();
   for (var i = 2; i < Math.Sqrt(n); i++)
   {
	   if (!marked[i]) continue;
	   for(int j = 0, factor = NextFactor(i, j); factor <= n; factor = NextFactor(i, ++j))
	   {
       marked[factor] = false;
	   }
   }
   int NextFactor(int i, int j) => i * i + j * i;

   //show the primes
   for (var i = 2; i <= n; i++)
   {
	   if(marked[i]) Console.WriteLine($"Prime number: {i}");
   }

OS project/utility of the week

https://benchmarkdotnet.org/

BenchmarkDotNet helps you to transform methods into benchmarks, track their performance, and share reproducible measurement experiments.

Who uses BenchmarkDotNet?

Everyone! BenchmarkDotNet is already adopted by more than 6800+ projects including dotnet/performance (reference benchmarks for all .NET Runtimes), dotnet/runtime (.NET Core runtime and libraries), Roslyn (C# and Visual Basic compiler), Mono, ASP.NET Core, ML.NET, Entity Framework Core, PowerShell SignalR, F#, Orleans, Newtonsoft.Json, Elasticsearch.Net, Dapper, Expecto, ImageSharp, RavenDB, NodaTime, Jint, NServiceBus, Serilog, Autofac, Npgsql, Avalonia, ReactiveUI, SharpZipLib, LiteDB, GraphQL for .NET, .NET Docs, RestSharp, MediatR, TensorFlow.NET, Apache Thrift. On GitHub, you can find 4500+ issues, 2500+ commits, and 500,000+ files that involve BenchmarkDotNet.